Escalando números

A lei Weber-Fechner (WF) é uma velha conhecida dos fisiologistas e psicólogos. Basicamente o que ela nos diz é que a menor diferença detectável pelos nossos sentidos (limiar de percepção) entre dois estímulos de intensidades similares é proporcional à intensidade do estímulo.

Isso faz, por exemplo, que a diferença percebida entre um estímulo de 1 unidade física de medida e outro de 10 unidades seja a mesma diferença percebida entre um estímulo de 10 unidades e outro de 100 unidades: (10-1)/10 = (100-10)/100.

Uma ampla gama de canais sensórios funciona segundo esse princípio: a percepção visual, a térmica, a auditiva, a olfativa, etc. (Ao menos como uma primeira aproximação. Segundo alguns autores, a relação não se mantém constante.)

Até mesmo na contagem a lei WF parece se aplicar. A indivíduos da tribo amazônica munduruku, sem educação formal, foi pedido que associassem certas quantidades de objetos que lhes eram apresentadas com a posição ao longo de uma reta. Os pontos não foram uniformemente espaçados como em uma reta dos números naturais, as distâncias entre os pontos representando as quantidades eram proporcionais às quantidades representadas: a distância entre 2 e 4 era a mesma da entre 4 e 8; a entre 1 e 4 era a mesma da entre 2 e 8 e assim por diante (e ambos tinham uma distância igual ao dobro da distância entre 2 e 4).

Nos casos de percepção de luminosidade, intensidade sonora, massa de objetos, acidez, dulçor, etc. grande parte da codificação que resulta no efeito WF ocorre nos próprios receptores - com as fibras nervosas disparando em uma função logarítmica com a intensidade do estímulo. Mas como funcionaria o processamento de informação abstrata como quantidade numérica de objetos - sem sensores específicos para sua percepção?

Parte da base fisiológica desse fenômeno foi desvendada em macacos resos. Eletrodos foram inseridos em uma região do córtex pré-frontal de sujeitos experimentais. Esses eletrodos mediam a atividades de neurônios quando eram apresentados aos macacos pontos em um monitor. Os pontos variavam aleatoriamente de um a cinco a cada exibição. As posições dos pontos na tela também variavam aleatoriamente. Alguns neurônios exibiam maior atividade quando uma determinada quantidade de pontos era exibida - respondiam a outras quantidades também, mas em menor intensidade (e menor a intensidade quanto maior a diferença do número de pontos exibidos em relação à quantidade para a qual a resposta do neurônio era a maior): para cada quantidade, havia um grupo de neurônios que exibiam maior resposta.

Quando os dados de atividade dos neurônios eram plotados contra a quantidade de objetos exibidos, as curvas de atividade resultantes eram mais simétricas quando o eixo da quantidade de objetos exibidos era apresentado em escala logarítmica. Isso parece indicar que a própria atividade dos neurônios obedecem à lei WF, já que em uma escala logarítmica uma distância fixa corresponde a uma proporção fixa: a distância entre 1 e 10 é a mesma da distância entre 10 e 100.

Mas se a escala logarítmica nos parece tão natural - não apenas nossos sentidos processam assim a informação e animais não-humanos também exibem essa característica, como humanos sem instrução formal parecem adotar essa escala para comparar valores - por que a noção de logaritmo aparece tão tardiamente na história da matemática? E mais, a escolha de introduzi-la também tardiamente no ensino (seguindo mais ou menos a ordem cronológica do desenvolvimento histórico dos conceitos matemáticos) é a mais proveitosa (Figura 1)?

Figura 1. Relação temporal histórico e educacional da descoberta e ensino de conceitos matemáticos. (Modificado de Mesoudi 2011)

A instrução formal deve ter um efeito direto sobre a perda do efeito WF na quantificação. Um procedimento similar ao realizado com o mundurukus com crianças americanas no jardim de infância, primeiro ano e segundo ano do nível básico de ensino revelou um mudança gradual no padrão - da relação logarítima para a linear (Figura 2). (Uma questão interessante é como se alterariam os padrões de funcionamento dos neurônios correspondentes ao do estudo com macacos-reso. Há uma restrição ética,no entanto, quanto a se introduzir eletrodos no cérebro de crianças. Seria possível treinar macacos a quantificarem de modo linear?)

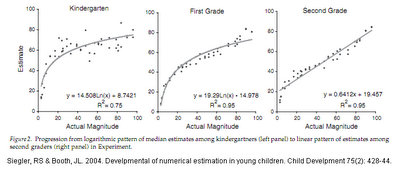
Figura 2. Modificação do padrão de avaliação de quantidade em crianças nos anos iniciais de estudo formal: esquerda) jardim de infância, meio) primeiro ano, direita) segundo ano do nível básico. (Fonte: Siegler & Booth 2004.)

Ao mesmo tempo, muitos autores e pesquisadores de matemática relatam que o conceito de função logarítmica é um dos que apresentam maiores dificuldades aos estudantes. Vários autores preferem até mesmo definir logaritmos naturais (ou neperianos) em termos de uma integral (o que sugere que eles achem o conceito de integral mais simples do que de logaritmo). Um efeito indireto do processo educacional?

Há algumas especulações a respeito da vantagem evolutiva do funcionamento do sistema sensório e do processamento de algumas informações sob o princípio WF (lembrando que há quem conteste que o modelo sugerido pelas lei WF descreva bem o padrão real). Uma das hipóteses é que a seleção natural haja no sentido de minimizar o erro relativo da avaliação da grandeza. Nesse caso ficaria a pergunta de por que o erro relativo seria uma característica importante ao indivíduo a ponto de ser alvo de seleção. Uma possível resposta é que o tamanho absoluto do erro que traz diferença significativa ao indivíduo depende do contexto dado pela intensidade do estímulo. Por exemplos: se em uma dada estação a quantidade de comida é escassa, qualquer grão de alimento desperdiçado pode ter consequências graves à sobrevivência ou ao sucesso reprodutivo do indivíduo, mas em uma estação relativamente abundante em recursos, a energia gasta para obter uma migalha a mais não compensaria; se há um predador por perto, o aparecimento de mais um dobram o perigo a que o sujeito está exposto, mas o aparecimento de um predador a mais em meio a outros 10 que já estão no local não faz tanta diferença no grau de perigo.

Mas mesmo derivada de observações empíricas que remontam a pelo menos 1760, a lei Weber-Fechner parece ser ainda um campo amplo para muita pesquisa. De um lado, se ela realmente se aplica para organismos vivos (e para quais subsistemas dos organismos ela se aplica); de outro, caso ela seja uma lei válida ao mundo vivo, destrinchar os detalhes fisiológicos da codificação e interpretação dos sinais segundo o princípio WF e, mais profundamente, os mecanismos e processos evolutivos que levaram ao funcionamento dos sistemas vivos segundo WF.