Como é que é? - Todo grande crescimento é exponencial e todo crescimento exponencial é grande?

Lemos em uma reportagem no Estadão:
"Um ex-traficante de Heliópolis, na zona sul, que começou no tráfico em 2002 e ali trabalhou até o ano passado, quando se tornou evangélico, conta que o crescimento das bocas foi exponencial. No começo do ano 2000, segundo ele, eram duas bocas maiores, que brigavam entre si. Atualmente, pouco antes de sair, o total de vendedores já havia passado dos 50." (grifos meus)


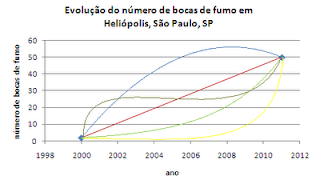
Pode até ser que tenha ocorrido crescimento de forma exponencial, mas apenas com esses dados não é possível saber. Na Figura 1, os dois dados estão plotados e vemos como vários tipos de curvas podem ser ajustadaos - a exponencial é a verde, mas há a linear em vermelho, e mais duas outras e uma infinidade (infinitas curvas mesmo) de outras curvas não representadas.

Figura 1. Exemplos de curvas que poderiam explicar o modo de crescimento das bocas de fumo no bairro de Heliópolis, na Zona Sul de São Paulo, SP.

Um crescimento exponencial (bem como de decaimento exponencial) ocorre quando a taxa de variação do valor de uma variável é uma proporção fixa em relação ao próprio valor da variável: naturalmente a taxa é positiva no crescimento e negativa no decaimento. Por exemplo, se a taxa de inflação anual é fixa em, digamos, 2%, ao longo do tempo, os preços médios dos produtos terão um aumento exponencial.


A curva é descrita por funções na forma:
N(t) = N(0).e^λt


Sendo N(t) o valor da grandeza no tempo t, N(0) o valor inicial, e é o número de Euler, λ é uma constante (de crescimento, se positiva, ou de decaimento, se negativa) e t é o tempo decorrido desde o início.


Precisamos de pelo menos mais um valor intermediário para ter uma confiança maior em se é mesmo exponencial ou não. Por exemplo, se para o ano 2006, o número de bocas de fumo tiver sido próximo a 30, não é compatível com um crescimento exponencial; se o valor for próximo a 10, sim. (Ainda assim haveria um sem número de outras curvas compatíveis com esses três pontos, mas eliminaríamos várias possibilidades.)


Em outra reportagem lemos:
"Essa obra, aclamada por dirigentes como o maior legado de Andrés Sanchez além do estádio em Itaquera, foi também responsável pelo lado 'ruim' da atual administração: o aumento exponencial da dívida.Ela praticamente dobrou de tamanho de 2007 a 2011, segundo dados preliminares do departamento financeiro do clube.O passivo passou de R$ 100 milhões para R$ 190 milhões."


Novamente, temos apenas dois pontos. Felizmente, alhures* temos a série completa entre 2007 e 2011 da evolução da dívida do clube paulista. Na Figura 2 estão representados tanto os valores contabilizados quanto a curva exponencial (em vermelho - em azul, curva de ajuste polinomial de terceira ordem):

Figura 2. Evolução da dívida do Sport Club Corinthians Paulista.

Os valores não se ajusteam tão bem a um modelo de crescimento exponencial - embora seja uma dívida crescente (e o indicativo para os anos imediatamente subsequentes é de um crescimento em ritmo maior do que o exponencial). Verdade que também não se ajustam tão mal - com um índice de correlação de 0,84 - e é um modelo mais simples do que o ajuste polinomial; mas um ajuste linear (não mostrado), não é muito pior - 0,82 - e é bem mais simples.


Em mais uma reportagem ainda:
"Esse aumento exponencial do risco regulatório na Argentina acaba por prejudicar os outros países latino-americanos, inclusive o Brasil."


Não temos nenhum dado apresentado ali de medida de risco regulatório. Há vários riscos com procedimentos de quantificação, não sei se os que envolvem questões de regulação de mercados está entre eles. Mas o uso neste caso de "aumento exponencial" é claramente metafórico. Esse uso tem se tornado comum com o sentido de uma variação rápida com potencial de se atingir valores muito grandes em curto período de tempo. Porém, o quão rapidamente o crescimento exponencial levará a grandes números varia com o valor de λ. Um valor suficientemente baixo pode levar a uma taxa decepcionantemente baixa e frustrar as expectativas que se têm quando se usa a expressão "aumento exponencial", como nesta tirinha do xkcd:

(Juros compostos - ou juros sobre juros - é uma das formas de funções exponenciais. Dívidas roladas, por sua vez, especialmente no cartão de crédito e em cheques especiais, costumam ter λ grandes o suficiente para se tornarem rapidamente impagáveis - algo como 10% ao mês em alguns bancos. Figura 3.)

Figura 3. Evolução da dívida ao longo de um ano de acordo com a taxa mensal de juros.

*Obs: Os valores podem ser conferidos aqui, aqui e aqui.