Ciência é prioridade? (parte 5)

Falei sobre a expectativa de ganho médio na postagem anterior e agora iremos ver o ótimo de Pareto.

O ótimo de Pareto em um sistema é alcançado quando qualquer melhora na condição de um elemento implique em uma piora em outro elemento do sistema. Embora seja uma noção originalmente aplicada em análise econômica, esse conceito é aplicável em uma ampla variedade de áreas. Deve-se notar que o ótimo de Pareto não implica em equidade ou em otimização global.

Interessante ilustração de ótimos de Pareto encontra-se na figura 1 desta página: reproduzo abaixo uma adaptação.

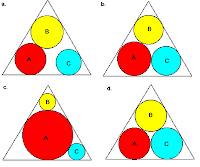Figura 1. Ótimo de Pareto. Três círculos internos a um triângulo. Objetivo: cada círculo deve ter a maior área possível; restrição: não pode haver sobreposição. (a.) Situação não-ótima: o círculo C pode ter sua área aumentada sem prejuízo aos demais círculos; (b.), (c.) e (d.) Situações ótimas. (c.) Ótimo global: a soma das áreas dos círculos é maximizada; (d.) Equidade: as áreas dos círculos são iguais. Adaptado de Petrie et al. 1995.

Um exemplo envolvendo o equilíbrio de Pareto pela alocação de recursos envolvendo agentes conscientes pode ser uma relação de troca entre dois indivíduos.

Caso 1) Digamos que Alexandre tenha 50 sapatos e Bianca tenha também 50 sapatos - todos do mesmo modelo e tamanho dos sapatos de Alexandre. Mas Alexandre tem 50 sapatos para pé esquerdo (A50E) e Bianca tem 50 sapatos para pé direito (B50D). Uma solução simples é que eles troquem entre si 25 sapatos de cada conjunto. Cada um ficará com 25 pares para os dois pés (A25E' + A25D'; B25E' + B25D'). A situação incial é de não-equilíbrio de Pareto (ou situação não-ótima), a situação em que ambos têm 25 pares de calçados é de equilíbrio.

Caso 2) Consideremos agora que Alexandre tenha 50 sapatos para pé esquerdo (A50E) e Bianca tenha 50 sapatos - 25 para pé esquerdo e 25 para pé direito (B25E + B25D). Essa é uma situação de equilíbrio de Pareto: Alexandre não pode trocar sapatos para pé esquerdo sem que Bianca piore sua situação (A50E'; B25E' + B25D').

Caso 3) Uma outra possibilidade seria: A50E e B24E + B26D. A situação de equilíbrio seria: A49E' + A1D'; B25E' + B25D'.

Caso 4) E neste caso: A50E e B24E + B25D? A situação de equilíbrio é: A49E' + A1D'; B25E' + B24D'. Repare que Bianca não ganha com a troca (considerando-se aqui apenas a questão de ter pares de sapatos utilizáveis), mas Alexandre consegue formar um par.

Estamos aqui assumindo que as operações de troca tenham o mesmo custo para ambas as partes e, mais, que cada sapato tenha o mesmo valor para cada um independentemente da distribuição. Isso não é realista, em especial a segunda suposição. Reanalisemos o caso 4. Bianca não ganha nada com a troca, Alexandre, no entanto, tem um interesse bastante grande. Por outro lado, Alexandre tem uma quantidade de sapatos esquerdos muito grande - Bianca poderia, em vez de aceitar uma troca 1 a 1, jogar o 'preço' do pé direito para o alto: ela poderia exigir 2 sapatos esquerdos em troca ou até mais. Alexandre ainda sairia ganhando - os pés esquerdos não lhe seriam úteis de qualquer forma.

Esse raciocínio vale para situações mais reais - substituindo sapatos esquerdos e direitos por produto x dinheiro; salário x tempo; recurso x resultado...

Uma situação de melhoria de Pareto potencial envolve um ganho por partes do sistema que seja igual ou maior do que a soma das perdas por outras partes do sistema.

Com as duas ferramentas: expectativa de ganho médio e do ótimo de pareto, poderemos analisar a otimização da distribuição de recursos, tendo como base de otimização a grande premissa: "é prioridade ajudar os necessitados".

Upideite(07/fev/2010): A versão inicial desta postagem incluía uma figura 2 sobre equilíbrio de Pareto em relações de troca, mas ela estava errada.

Parte 6